Data Structure Asymptotic Notation

Asymptotic Notations are the expressions that are used to represent the complexity of an algorithm.

As we discussed in the last tutorial, there are three types of analysis that we perform on a particular algorithm.
Best Case: In which we analyse the performance of an algorithm for the input, for which the algorithm takes less time or space.

Worst Case: In which we analyse the performance of an algorithm for the input, for which the algorithm takes long time or space.

Average Case: In which we analyse the performance of an algorithm for the input, for which the algorithm takes time or space that lies between best and worst case.

Types of Data Structure Asymptotic Notation

1. Big-O Notation (Ο) – Big O notation specifically describes worst case scenario.
2. Omega Notation (Ω) – Omega(Ω) notation specifically describes best case scenario.
3. Theta Notation (θ) – This notation represents the average complexity of an algorithm.

Big-O Notation (Ο)

Big O notation specifically describes worst case scenario. It represents the upper bound running time complexity of an algorithm. Lets take few examples to understand how we represent the time and space complexity using Big O notation.

O(1)

Big O notation O(1) represents the complexity of an algorithm that always execute in same time or space regardless of the input data.

O(1) example
The following step will always execute in same time(or space) regardless of the size of input data.

Accessing array index(int num = arr[5])

O(n)

Big O notation O(N) represents the complexity of an algorithm, whose performance will grow linearly (in direct proportion) to the size of the input data.

O(n) example
The execution time will depend on the size of array. When the size of the array increases, the execution time will also increase in the same proportion (linearly)

Traversing an array

O(n^2)

Big O notation O(n^2) represents the complexity of an algorithm, whose performance is directly proportional to the square of the size of the input data.

O(n^2) example

Traversing a 2D array

Other examples: Bubble sort, insertion sort and selection sort algorithms (we will discuss these algorithms later in separate tutorials)

Similarly there are other Big O notations such as:
logarithmic growth O(log n), log-linear growth O(n log n), exponential growth O(2^n) and factorial growth O(n!).

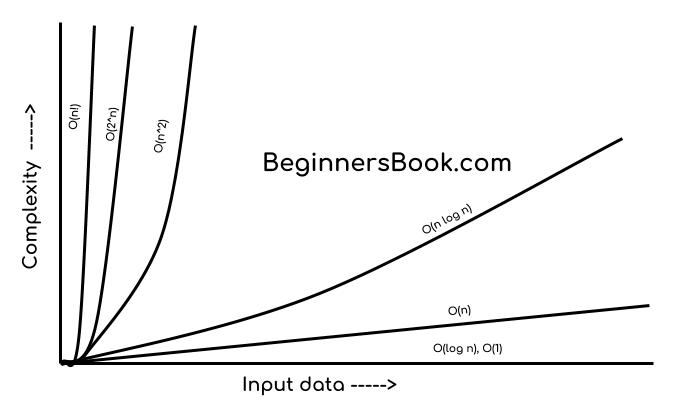
If I have to draw a diagram to compare the performance of algorithms denoted by these notations, then I would draw it like this:

O(1) < O(log n) < O (n) < O(n log n) < O(n^2) < O (n^3)< O(2^n) < O(n!)

Omega Notation (Ω)

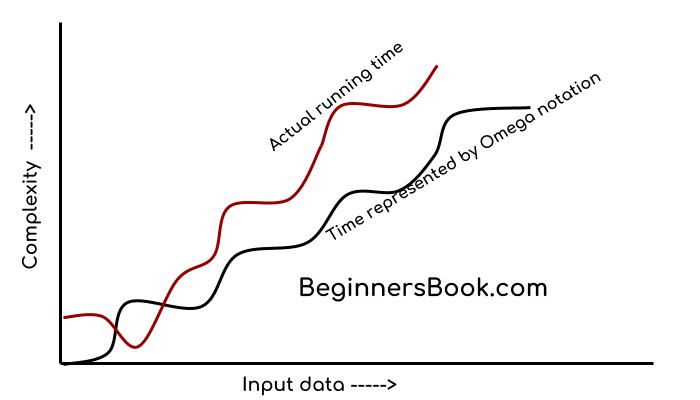
Omega notation specifically describes best case scenario. It represents the lower bound running time complexity of an algorithm. So if we represent a complexity of an algorithm in Omega notation, it means that the algorithm cannot be completed in less time than this, it would at-least take the time represented by Omega notation or it can take more (when not in best case scenario).

Theta Notation (θ)

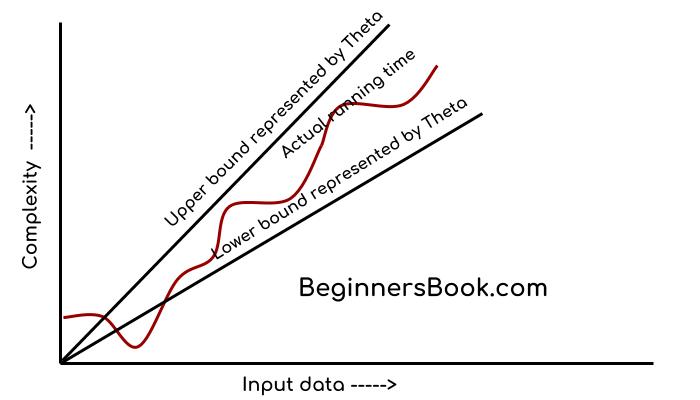
This notation describes both upper bound and lower bound of an algorithm so we can say that it defines exact asymptotic behaviour. In the real case scenario the algorithm not always run on best and worst cases, the average running time lies between best and worst and can be represented by the theta notation.