In this guide, you will learn recursion in C programming with the help of examples. A function that calls itself is known as recursive function and this process of calling itself is called recursion.
Recursion Example 1: Fibonacci sequence
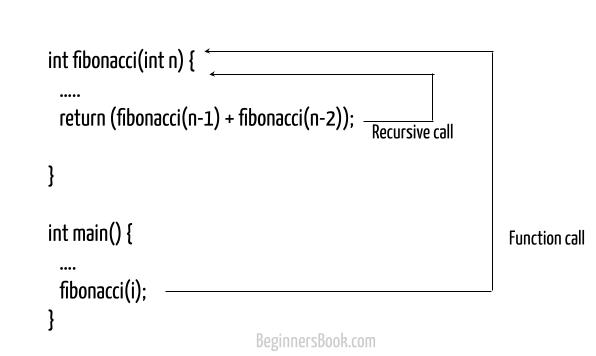
In this example, we are displaying Fibonacci sequence using recursion. The Fibonacci Sequence is the series of numbers where each number is sum of previous two numbers, for example: 0, 1, 1, 2, 3, 5, 8, ...
The first term 0 and second term 1 needs to be specified, third term onwards, the number is equivalent to the sum of previous two numbers. Here we are finding the previous two terms by calling the same function like this: fibonacci(n-1) and fibonacci(n-2).
#include <stdio.h>
//recursive function, this function is calling itself
int fibonacci(int n) {
if(n == 0){
return 0;
} else if(n == 1) {
return 1;
} else {
return (fibonacci(n-1) + fibonacci(n-2));
}
}
int main() {
int n = 8;
int i;
printf("Fibonacci sequence of %d terms: " , n);
for(i = 0;i<n;i++) {
printf("%d ",fibonacci(i));
}
}
Output:
Fibonacci sequence of 8 terms: 0 1 1 2 3 5 8 13
Recursion Example 2: Factorial
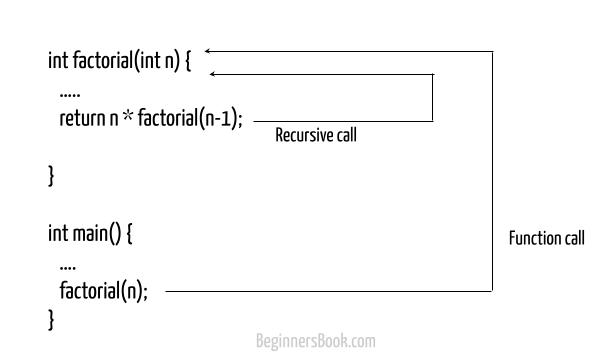
We find the factorial like this:
Factorial of n! = (n) * (n-1) * ... * 1
We can simply this formula as: factorial of n = n * factorial of (n-1)
Factorial of n! = (n) * (n-1)!
This logic can be implemented in a C program using recursion. The factorial(n) calls factorial(n-1), factorial(n-1) calls factorial(n-2) and so on until the base case is hit when n becomes zero which returns 1.
#include <stdio.h>
//recursive function
int factorial(int n) {
//base case
if(n == 0) {
return 1;
} else {
//calling itself
return n * factorial(n-1);
}
}
int main() {
int num = 4;
printf("Factorial of %d is: %d\n" , num , factorial(num));
}
Output:
Factorial of 4 is: 24
When can we use recursion?
Recursion can be used for solving problems that can be broken down into smaller, repetitive problems. In our example of factorial, we knew that factorial of n is dependent on factorial of n-1 and so on. So we used recursion to solve that problem.
Similarly, in fibonacci series example, we understood that a number in series is sum of previous two numbers, which means any number of fibonacci series can be broken down from right to left by finding the previous two numbers.
Advantages and Disadvantages of Recursion
Advantages:
1. Code is easier to write. Instead of creating several functions for a same problem, a single function is used to solve the complete problem.
2. Frequently used in tree traversal as the root node of tree has child nodes, these child nodes have leaf nodes. This is easier to implement using recursion rather than any other programming technique.
Disadvantages:
1. Makes the code difficult to analyse.
2. Uses more memory as the repetitive calls keeps on using the memory.
3. Can run in an infinite loop if not coded properly.
Leave a Reply